AlgorithmsBranch and Bound

The Traveling Salesperson Problem(외판원 문제)

분기한정법, 알고리즘

Suppose a salesperson is planning a sales trip that includes 20 cities. Each city is connected to some of the other cities by a road. To minimize travel time, we want to determine a shortest route that starts at the salesperson’s home city, visits each of the cities once, and ends up at the home city. This problem of determining a shortest route is called the Traveling Salesperson problem.

Recall that the goal in this problem is to find the shortest path in a directed graph that starts at a given vertex, visits each vertex in the graph exactly once, and ends up back at the starting vertex. Such a path is called an optimal tour. Because it does not matter where we start, the starting vertex can simply be the first vertex.

외판원 문제는 여러 도시들이 있고 한 도시에서 다른 도시로 이동하는 비용이 모두 주어졌을 때, 모든 도시들을 단 한번씩만 방문하고 원래 시작점으로 돌아오는 최적여행경로(최소비용의 이동 순서)를 구하는 것이다.

외판원 문제는 0-1 Knapsack 문제와 함께 NP-Complete에 속한다.

Example Shows the adjacency matrix representation of a graph containing five vertices, in which there is an edge from every vertex to every other vertex, and an optimal tour for that graph.

[Adjacency matrix representation of a graph that has an edge from every vertex to every other vertex(left), and the nodes in the graph and the edges in an optimal tour(right)]

Step 1 [1]을 포함하는 노드를 방문한다. (일주여행경로의 첫번째 정점으로 $v_1$을 선택)

v1 minimum(14, 4, 10, 20) = 4 // 최소값 계산시 자기자신 제외
v2 minimum(14, 7, 8, 7)   = 7 // 최소값 계산시 자기자신 제외
v3 minimum(4, 5, 7, 16)   = 4 // 최소값 계산시 자기자신 제외
v4 minimum(11, 7, 9, 2)   = 2 // 최소값 계산시 자기자신 제외
v5 minimum(18, 7, 17, 4)  = 4 // 최소값 계산시 자기자신 제외

[1]을 포함한 노드에서 확장하여 구한 일주여행경로길이의 bound = 21
minlength = ∞

Step 2 [1, 2]를 포함하는 노드를 방문한다. (일주여행경로의 두 번째 정점으로 $v_2$ 선택)

v1                     14 // v1 -> v2는 확정이므로 14
v2 minimum(7, 8, 7)   = 7 // 최소값 계산시 자기자신과 v1제외(사이클 방지)
v3 minimum(4, 7, 16)  = 4 // 최소값 계산시 자기자신과 이미 방문한 v2 제외
v4 minimum(11, 9, 2)  = 2 // 최소값 계산시 자기자신과 이미 방문한 v2 제외
v5 minimum(18, 17, 4) = 4 // 최소값 계산시 자기자신과 이미 방문한 v2 제외

[1, 2]를 포함한 노드에서 확장하여 구한 일주여행경로길이의 bound = 31

Step 3 [1, 3]을 포함하는 노드를 방문한다. (일주여행경로의 두 번째 정점으로 $v_3$ 선택)

v1                      4 // v1 -> v3는 확정이므로 4
v2 minimum(14, 8, 7)  = 7 // 최소값 계산시 자기자신과 이미 방문한 v3 제외
v3 minimum(5, 7, 16)  = 5 // 최소값 계산시 자기자신과 시작점 v1 제외(사이클 방지)
v4 minimum(11, 7, 2)  = 2 // 최소값 계산시 자기자신과 이미 방문한 v3 제외
v5 minimum(18, 7, 4)  = 4 // 최소값 계산시 자기자신과 이미 방문한 v3 제외

[1, 3]를 포함한 노드에서 확장하여 구한 일주여행경로길이의 bound = 22

Step 4~5 [1, 4], [1, 5] 방문은 Step2~3과 비슷하므로 생략

Step 6 bound 값이 가장 작으면서 유망하고 확장하지 않은 노드를 결정한다. 그 노드는 [1, 3]을 포함하는 노드이다. 그 노드의 자식노드부터 방문한다.

Step 7 [1, 3, 2]를 포함하는 노드를 방문한다. (일주여행경로의 세 번째 정점으로 $v_2$ 선택)

v1                   4 // v1 -> v3는 확정이므로 4
v2 minimum(8, 7)   = 7 // 최소값 계산시 자기자신과 이미 방문한 v3, 시작점 v1 제외
v3                   5 // v3 -> v2는 확정이므로 5
v4 minimum(11, 2)  = 2 // 최소값 계산시 자기자신과 이미 방문한 v3, v2는 제외
v5 minimum(18, 4)  = 4 // 최소값 계산시 자기자신과 이미 방문한 v3, v2는 제외

[1, 3, 2]를 포함한 노드에서 확장하여 구한 일주여행경로길이의 bound = 22

Step 8 [1, 3, 4]를 포함하는 노드를 방문한다. (일주여행경로의 세 번째 정점으로 $v_4$ 선택)

v1                   4 // v1 -> v3는 확정이므로 4
v2 minimum(14, 7)  = 7 // 최소값 계산시 자기자신과 이미 방문한 v3, v4 제외
v3                   7 // v3 -> v4는 확정이므로 7
v4 minimum(7, 2)   = 2 // 최소값 계산시 자기자신과 이미 방문한 v3, 시작점 v1 제외
v5 minimum(18, 7)  = 7 // 최소값 계산시 자기자신과 이미 방문한 v3, v4 제외

[1, 3, 4]를 포함한 노드에서 확장하여 구한 일주여행경로길이의 bound = 27

Step 9 [1, 3, 5] 방문은 Step 7~8과 비슷하므로 생략

Step10 bound 값이 가장 작으면서 유망하고 확장하지 않은 노드를 결정한다. 그 노드는 [1, 3, 2]를 포함하는 노드이다. 그 노드의 자식노드부터 방문한다.

Step11 [1, 3, 2, 4]를 포함하는 노드를 방문한다. (일주여행경로의 네 번째 정점으로 $v_4$ 선택) 이때 남은 정점은 $v_5$하나이므로 [1, 3, 2, 4, 5, 1]이라는 일주여행경로가 확정된다.

[1, 3, 2, 4, 5, 1] 일주여행경로의 길이를 계산하면 37(=4+5+8+2+18)이 된다.
37 < minlength = ∞ →  minlength = 37
[1, 5] bound = 42 >= minlength = 37 // [1, 5]는 이 시점에서 유망하지 않다.
[1, 3, 5] bound = 39 >= minlength = 37 // [1, 3, 5]는 이 시점에서 유망하지 않다.

Step12 [1, 3, 2, 5]를 포함하는 노드를 방문한다. (일주여행경로의 네 번째 정점으로 $v_5$ 선택) 이때 남은 정점은 $v_4$하나이므로 [1, 3, 2, 5, 4, 1]이라는 일주여행경로가 확정된다.

[1, 3, 2, 5, 4, 1] 일주여행경로의 길이를 계산하면 31(=4+5+7+4+11)이 된다.
31 < minlength = 37 →  minlength = 31
[1, 2] bound = 31 >= minlength = 31 // [1, 2]는 이 시점에서 유망하지 않다.

Step13 bound 값이 가장 작으면서 유망하고 확장하지 않은 노드를 결정한다. 그 노드는 [1, 3, 4]를 포함하는 노드이다. 그 노드의 자식노드부터 방문한다.

Step14 [1, 3, 4, 2]를 포함하는 노드를 방문한다. 이때 남은 정점은 $v_5$하나이므로 [1, 3, 4, 2, 5, 1]이라는 일주여행경로가 확정된다.

[1, 3, 4, 2, 5, 1] 일주여행경로의 길이를 계산하면 43(=4+7+7+7+18)이 된다.

Step15 [1, 3, 4, 5]를 포함하는 노드를 방문한다. 이때 남은 정점은 $v_2$하나이므로 [1, 3, 4, 5, 2, 1]이라는 일주여행경로가 확정된다.

[1, 3, 4, 5, 2, 1] 일주여행경로의 길이를 계산하면 34(=4+7+2+7+14)가 된다.

Step16 bound 값이 가장 작으면서 유망하고 확장하지 않은 노드를 결정한다. [1, 4]를 포함하는 노드가 유일하다. 그 노드의 자식노드부터 방문한다.

Step17 [1, 4, 2]를 포함하는 노드를 방문한다.

v1                   10 // v1 -> v4는 확정이므로 10
v2 minimum(7, 7)   =  7 // 최소값 계산시 자기자신과 이미 방문한 v4, 시작점 v1 제외
v3 minimum(4, 16)  =  4 // 최소값 계산시 자기자신과 이미 방문한 v4, v2 제외
v4                 =  7 // v4 -> v2는 확정이므로 7
v5 minimum(18, 17) = 17 // 최소값 계산시 자기자신과 이미 방문한 v4, v2 제외

[1, 4, 2] bound = 45 >= minlength = 31 // [1, 4, 2]는 유망하지 않다.

Step18 [1, 4, 3]를 포함하는 노드를 방문한다.

v1                   10 // v1 -> v4는 확정이므로 10
v2 minimum(14, 7)  =  7 // 최소값 계산시 자기자신과 이미 방문한 v4, v3 제외
v3 minimum(5, 16)  =  5 // 최소값 계산시 자기자신과 이미 방문한 v4, 시작점 v1 제외
v4                 =  9 // v4 -> v3는 확정이므로 9
v5 minimum(18, 7)  =  7 // 최소값 계산시 자기자신과 이미 방문한 v4, v3 제외

[1, 4, 3] bound = 38 >= minlength = 31 // [1, 4, 3]은 유망하지 않다.

Step19 [1, 4, 5]를 포함하는 노드를 방문한다.

v1                   10 // v1 -> v4는 확정이므로 10
v2 minimum(14, 7)  =  7 // 최소값 계산시 자기자신과 이미 방문한 v4, v5 제외
v3 minimum(4, 5)   =  4 // 최소값 계산시 자기자신과 이미 방문한 v4, v5 제외
v4                 =  2 // v4 -> v5는 확정이므로 2
v5 minimum(7, 17)  =  7 // 최소값 계산시 자기자신과 이미 방문한 v4, 시작점 v1 제외

[1, 4, 5]를 포함한 노드에서 확장하여 구한 일주여행경로길이의 bound = 30

Step20 bound 값이 가장 작으면서 유망하고 확장하지 않은 노드를 결정한다. [1, 4, 5]를 포함하는 노드가 유일하다. 그 노드의 자식노드부터 방문한다.

Step21 [1, 4, 5, 2]를 포함하는 노드를 방문한다. 이때 남은 정점은 $v_3$하나이므로 [1, 4, 5, 2, 3, 1]이라는 일주여행경로가 확정된다.

[1, 4, 5, 2, 3, 1] 일주여행경로의 길이를 계산하면 30(=10+2+7+7+4)이 된다.
30 < minlength = 31 →  minlength = 30

Step22 [1, 4, 5, 3]을 포함하는 노드를 방문한다. 이때 남은 정점은 $v_2$하나이므로 [1, 4, 5, 3, 2, 1]이라는 일주여행경로가 확정된다.

[1, 4, 5, 3, 2, 1] 일주여행경로의 길이를 계산하면 48(=10+2+17+5+14)이 된다.

Step23 bound 값이 가장 작으면서 유망하고 확장하지 않은 노드를 결정한다. 해당하는 노드가 없으므로 알고리즘은 종료된다. 일주여행경로 [1, 4, 5, 2]를 포함하는 노드가 최적 일주여행경로([1, 4, 5, 2, 3, 1])이고, 그 길이는 30이다.

[The pruned state space tree produced using best-first search with branch-and-bound pruning in this Example. At each node that is not a leaf in the state space tree, the partial tour is at the top and the bound on the length of any tour that could be obtained by expanding beyond the node is at the bottom. At each leaf in the state space tree, the tour is at the top and its length is at the bottom. The node shaded in color is the one at which an optimal tour is found.]


The Best-First Search with Branch-and-Bound Pruning Algorithm for the Traveling Salesperson Problem

Algorithm Design

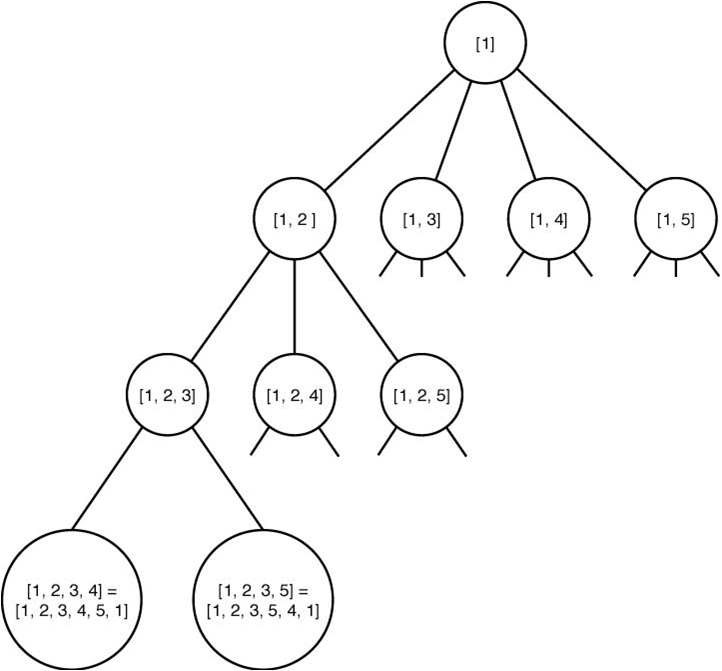
An obvious state space tree for this problem is one in which each vertex other than the starting one is tried as the first vertex (after the starting one) at level 1, each vertex other than the starting one and the one chosen at level 1 is tried as the second vertex at level 2, and so on. A portion of this state space tree, in which there are five vertices and in which there is an edge from every vertex to every other vertex, is shown in the below Figure. In what follows, the term “node” means a node in the state space tree, and the term “vertex” means a vertex in the graph. At each node in the below Figure, we have included the path chosen up to that node.

For simplicity, we have denoted a vertex in the graph simply by its index. A node that is not a leaf represents all those tours that start with the path stored at that node. For example, the node containing [1, 2, 3] represents all those tours that start with the path [1, 2, 3]. That is, it represents the tours [1, 2, 3, 4, 5, 1] and [1, 2, 3, 5, 4, 1]. Each leaf represents a tour. We need to find a leaf that contains an optimal tour. We stop expanding the tree when there are four vertices in the path stored at a node because, at that time, the fifth one is uniquely determined. For example, the far-left leaf represents the tour [1, 2, 3, 4, 5, 1] because once we have specified the path [1, 2, 3, 4], the next vertex must be the fifth one.

외판원 문제에 대한 상태공간 트리를 만드는 방법은 다음과 같다. 각 노드는 출발 노드로부터의 일주 여행 경로를 나타내게 된다. 예를 들어 루트노드의 여행 경로는 [1]이 되고, 루트노드에서 뻗어 나가는 레벨 1의 여행 경로는 각각 [1, 2], [1, 3], …, [1, 5]가 된다. 노드 [1, 2]에서 뻗어 나가는 레벨 2에 있는 노드들의 여행 경로는 각각 [1, 2, 3], …, [1, 2, 5]가 되며, 같은 방식으로 한 단계씩 레벨을 확장해 나가면서 잎노드에 도달하면 완전한 일주여행경로를 가지게 된다.

최적화된 일주여행경로를 구하기 위해서는 잎 노드에 있는 일주여행경로를 모두 검사하여 그 중에서 길이가 가장 짧은 값을 찾으면 된다.

To use best-first search, we need to be able to determine a bound for each node. we need to determine a lower bound on the length of any tour that can be obtained by expanding beyond a given node, and we call the node promising only if its bound is less than the current minimum tour length. We can obtain a bound as follows. In any tour, the length of the edge taken when leaving a vertex must be at least as great as the length of the shortest edge emanating from that vertex. Therefore, a lower bound on the cost (length of the edge taken) of leaving vertex $v_1$ is given by the minimum of all the nonzero entries in row 1 of the adjacency matrix, a lower bound on the cost of leaving vertex $v_2$ is given by the minimum of all the nonzero entries in row 2, and so on.

In the same way, we can obtain a lower bound on the length of a tour that can be obtained by expanding beyond any node in the state space tree, and we use these lower bounds in our best-first search.

bound 값을 계산하는 방법은 다음과 같다. 어떤 일주여행경로라도 한 정점을 떠날 때 선택한 이음선의 길이는 그 정점에서 나오는 가장 짧은 이음선의 길이만큼은 최소한 길다. 그러므로 정점 $v_1$을 떠나는 비용의 하한은 인접행렬의 첫 번째 행에서 0이 아닌 모든 값 중에서 최소값이 되고, $v_2$를 떠나는 비용의 하한은 인접행렬의 2번째 행에서 0이 아닌 모든 값 중에서 최소값이 되고, …, 이런 식으로 각 정점들에 대해 최소값을 계산한다. 각 일주여행경로는 정점을 정확히 각각 한 번씩 떠나야 하기 때문에, 일주여행경로 길이의 bound는 이 최소값들의 합이다.

같은 방법으로 상태공간트리에서 주어진 노드 이후로부터 확장하여 구할 수 있는 일주여행경로길이의 bound 값을 계산할 수 있고, 이 bound 값을 최고우선탐색에 사용할 수 있다.

v1 minimum(14, 4, 10, 20) = 4 // 최소값 계산시 자기자신 제외
v2 minimum(14, 7, 8, 7)   = 7 // 최소값 계산시 자기자신 제외
v3 minimum(4, 5, 7, 16)   = 4 // 최소값 계산시 자기자신 제외
v4 minimum(11, 7, 9, 2)   = 2 // 최소값 계산시 자기자신 제외
v5 minimum(18, 7, 17, 4)  = 4 // 최소값 계산시 자기자신 제외

[1]을 포함한 노드에서 확장하여 구한 일주여행경로길이의 bound = 21

v1                     14 // v1 -> v2는 확정이므로 14
v2 minimum(7, 8, 7)   = 7 // 최소값 계산시 자기자신과 시작점 v1제외(사이클 방지)
v3 minimum(4, 7, 16)  = 4 // 최소값 계산시 자기자신과 이미 방문한 v2 제외
v4 minimum(11, 9, 2)  = 2 // 최소값 계산시 자기자신과 이미 방문한 v2 제외
v5 minimum(18, 17, 4) = 4 // 최소값 계산시 자기자신과 이미 방문한 v2 제외

[1, 2]를 포함한 노드에서 확장하여 구한 일주여행경로길이의 bound = 31

v1                 14 // v1 -> v2는 확정이므로 14
v2                = 7 // v2 -> v3는 확정이므로 7
v3 minimum(7, 16) = 7 // 최소값 계산시 자기자신과 이미 방문한 v2, 시작점 v1 제외
v4 minimum(11, 2) = 2 // 최소값 계산시 자기자신과 이미 방문한 v2, v3 제외
v5 minimum(18, 4) = 4 // 최소값 계산시 자기자신과 이미 방문한 v2, v3 제외

[1, 2, 3]를 포함한 노드에서 확장하여 구한 일주여행경로길이의 bound = 34

Pseudo Code

// We will use the following data type in the algorithm.
struct node
{
  int level;
  ordered_set path;
  number bound;
}

void travel2(int n, const number W[][], ordered_set &opttour, number &minlength)
{
  priority_queue_of_node PQ;
  node u, v;

  initialize(PQ); // Initialize PQ to be empty.
  v.level = 0;
  v.path = [1]; // Make first vertex the starting one.
  v.bound = bound(v);
  minlength = INFINITE;
  insert(PQ, v);

  while (!empty(PQ))
  {
    remove(PQ, v); // Remove node with best bound.
    if (v.bound < minlength)
    {
      u.level = v.level + 1;
      for ((all i such that 2 < i < n) && (i is not in v.path))
      {
        // e.g. first copy [1 3] to make paths [1 3 2], [1 3 4], [1 3 5]
        u.path = v.path;    
        put i at the end of u.path;

        if (u.level == n-2)
        {
          // Check if next vertex completes a tour.
          put index of only vertex not in u.path at the end of u.path;
          put 1 at the end of u.path; // Make first vertex last one.

          // Function length computes the length of the tour.
          if (length(u) < minlength)  
          {
            minlength = length(u);
            opttour = u.path;
          }
        }
        else
        {
          u.bound = bound(u);
          if (u.bound < minlength)
            insert(PQ, u);
        }
      }
    }
  }
}

Source Code

// File: travel2.h
#ifndef TRAVELING_SALESPERSON_H
#define TRAVELING_SALESPERSON_H
#include "pqueue.h" // Provides priority_queue and node
#include "graph.h"  // Provides graph
using namespace data_structures; // for graph and node

namespace algorithms
{
  void travel2(const int n, graph W, std::vector<int>& opttour, int& minlength);
  // Problem: Determine an optimal tour in a weighted, directed graph. The weights
  // are nonnegative numbers.
  // Inputs: a weighted, directed graph, and n, the number of vertices in
  // the graph. The graph is represented by a graph class, which has both its
  // rows and columns indexed from 1 to n, where W.get_edge(i, j) is the weight
  // on the edge from the ith vertex to the jth vertex.
  // Outputs: variable minlength, whose value is the length of an optimal tour,
  // and variable optour, whose value is an optimal tour.

  int length(node u, graph W);
  // Inputs: a weighted, directed graph, and node.
  // Outputs: Returns the length of the tour u.path

  int bound(node u, graph W, const int n, int ptah_strt_vertex);
  // Inputs: a weighted, directed graph, node, and n, the number of vertices
  // in the graph.
  // Outputs: Returns the bound for a node.

  // Helper function
  int find_minedge_case1(graph W, int curr_vertex);
  int find_minedge_case2(graph W, int curr_vertex,
                         bool* visited, int path_strt_vertex);
  int find_minedge_case3(graph W, int curr_vertex,
                         bool* visited, int path_strt_vertex, node u);
  int find_unvisited_vertex(node u, const int n);
}

#endif
// File: travel2.cpp
#include "travel2.h"
#include <iostream>
#include <iomanip>
#include <cassert>
using namespace std;

namespace algorithms
{
  void travel2(const int n, graph W, vector<int>& opttour, int& minlength)
  {
    priority_queue PQ;
    node u, v;
    const int start_vertex = 1; // Make first vertex the starting one.

    assert(PQ.is_empty( )); // Initialize PQ to be empty.
    v.level = 0;
    v.path.push_back(start_vertex);
    v.bound = bound(v, W, n, start_vertex);
    minlength = W.INFINITE;
    PQ.insert(v);

    while (!PQ.is_empty( ))
    {  
      //PQ.print_tree("The tree:", 0);

      v = PQ.get_front( ); // Remove node with best bound.
      if (v.bound < minlength)
      {
        u.level = v.level + 1; // Set u to a child of v.

        for (int i = 1; i <= n; ++i)
        {
          bool visited = false;
          vector<int>::iterator itr;

          // Find i(2 <= i <= n) that is not in v.path
          for (itr = v.path.begin( ); itr != v.path.end( ); ++itr)
          {
            if (*itr == i)
              visited = true;
          }

          if (!visited)
          {
            // Copy and Put i at the end of u.path.
            u.path = v.path;
            u.path.push_back(i);

            // Check if next vertex completes a tour.
            if (u.level == n-2)
            {
              // Put index of only vertex not in u.path at the end of u.path.
              int last_vertex = find_unvisited_vertex(u, n);
              u.path.push_back(last_vertex);

              // Put 1 at the end of u.path. (Make first vertex last one)
              u.path.push_back(start_vertex);

              // Function length computes the length of the tour.
              int tour_length = length(u, W);
              if (tour_length < minlength)
              {
                minlength = tour_length;
                opttour = u.path;
              }
            }
            else
            {
              u.bound = bound(u, W, n, start_vertex);

              if (u.bound < minlength)
                PQ.insert(u);
            }

            cout << "[" ;

            vector<int>::iterator itr;
            for (itr = u.path.begin(); itr != u.path.end(); ++itr)
            {
              cout << *itr;    
              if (!(itr+1 == u.path.end()))
                cout << ", ";
            }
            cout <<  "]" << " Bound = " << bound(u, W, n, start_vertex);
            cout << ", minlenth = " << minlength << endl;
          }
        }
      }
      else
      {
        cout << "prunning is ... ";
        cout << "[" ;

        vector<int>::iterator itr;
        for (itr = v.path.begin(); itr != v.path.end(); ++itr)
        {
          cout << *itr;    
          if (!(itr+1 == v.path.end()))
            cout << ", ";
        }
          cout <<  "]" << " Bound = " << v.bound << " >= minlength"  << endl;

      }
    }
  }

  // Returns the bound for a node.
  int bound(node u, graph W, const int n, int path_strt_vertex)
  {
    int minimum;
    int answer = 0;
    bool* visited;
    vector<int>::iterator itr;

    visited = new bool[n]; // dynamic allocation
    --visited; // pointer offset

    // initialization
    for (int i = 1; i <= n; ++i)
      visited[i] = false;

    // marking only visited vertex e.g. [1,2]..
    for (itr = u.path.begin( ); itr != u.path.end( ); ++itr)
      visited[*itr] = true;

    for (int i = 1; i <= n; ++i) // n is equal to the number of vertices
    {
      minimum = W.INFINITE;

      if (u.path.capacity( ) == 1) // only one path exists
      {
        minimum = find_minedge_case1(W, i);
      }
      else
      {
        if (!visited[i]) // unvisted vertex_i -> find minimum edge
          minimum = find_minedge_case2(W, i, visited, path_strt_vertex);
        else // visited vertex_i -> (1 to i-1) determin. edge + find minimum edge
          minimum = find_minedge_case3(W, i, visited, path_strt_vertex, u);
      }

      answer += minimum;
    }

    delete [ ] (visited + 1); // deallocation
    return answer;
  }

  // Helper function
  int find_minedge_case1(graph W, int curr_vertex)
  {
    int minimum = W.INFINITE;  

    // CASE1 : Only one vertex exists in this path
    // e.g. path = [1], i = 1 -> minimum = min(v2, v3, v4, v5)
    //      path = [1], i = 2 -> minimum = min(v1, v3, v4, v5)
    //      ...
    //      path = [1], i = 5 -> minimum = min(v1, v2, v3, v4)

    for (int j = 1; j <= W.get_size( ); ++j)
    {
      if (curr_vertex != j && W.get_edge(curr_vertex, j) < minimum)
        minimum = W.get_edge(curr_vertex, j);
    }

    return minimum;
  }

  // Helper function
  int find_minedge_case2(graph W, int curr_vertex,
                         bool* visited, int path_strt_vertex)
  {
    int minimum = W.INFINITE;

    // CASE2 : i is one of unvisiteid vertexs.
     // e.g. path = [1, 2], i = 3 -> minimum = min(v1, v4, v5)
     //                     i = 4 -> minimum = min(v1, v3, v5)
     //                     i = 5 -> minimum = min(v1, v3, v4)
     // (j != start_vertex && visited[j]) is excluded from calculations

    for (int j = 1; j <= W.get_size( ); ++j)
    {
      if (curr_vertex != j && W.get_edge(curr_vertex, j) < minimum)
      {
        if (j != path_strt_vertex && visited[j])
          ; // do nothing
        else
          minimum = W.get_edge(curr_vertex, j);
      }
    }

    return minimum;
  }

  int find_minedge_case3(graph W, int curr_vertex,
                         bool* visited, int path_strt_vertex, node u)
  {
    int minimum = W.INFINITE;
    vector<int>::iterator curr_itr, next_itr;
    curr_itr = next_itr = u.path.begin( );

    // CASE3 : i is one of visited vertex.
    // e.g. path = [1, 2, 3], i = 1 -> minimum = graph.get_edge(1, 2)
    //                        i = 2 -> minimum = graph.get_edge(2, 3)
    //                        i = 3 -> minimum = min(v4, v5)
    // (j == path_strt_vertex || visited[j]) is excluded from calculations

    for (curr_itr = u.path.begin( ); curr_itr != u.path.end( ); ++curr_itr)
    {
      if (*curr_itr == curr_vertex)
      {
        next_itr = curr_itr + 1;

        if (next_itr != u.path.end( ))
        {
          // [1, 2, 3] -> get_edge(1, 2) and get_edge(2, 3)
          minimum = W.get_edge(*curr_itr, *next_itr);
          break;
        }
        else
        {
          for (int j = 1; j <= W.get_size( ); ++j)
          {
            if (curr_vertex != j  && W.get_edge(curr_vertex, j) < minimum)
            {
              if (j == path_strt_vertex || visited[j])
                ; // do nothing
              else
                minimum = W.get_edge(curr_vertex, j);
            }
          }

          break;   
        }
      }
    }

    return minimum;  
  }

  // Returns the length of the tour u.path
  int length(node u, graph W)
  {
    int answer = 0;
    vector<int>::iterator itr;
    vector<int>::iterator end_itr;

    for (itr = u.path.begin( ); itr != u.path.end( ); ++itr)
    {
      end_itr = itr;

      if ((itr + 1) == u.path.end( ))
        break;

      answer += W.get_edge(*itr, *(itr+1));
    }

    answer += W.get_edge(*end_itr, u.path.front( ));

    return answer;
  }

  // Helper function
  int find_unvisited_vertex(node u, const int n)
  {
    int unvisited_vertex;
    bool* visited = new bool[n];
    --visited; // pointer offset

    // initialization
    for (int j = 1; j <= n; ++j)
      visited[j] = false;

    // mark visited vertex
    for (vector<int>::iterator itr = u.path.begin( ); itr != u.path.end( ); ++itr)
    {
      for (int j = 1; j <=n ; ++j)
      {
        if (*itr == j)
        {
          visited[*itr] = true;
          break;
        }
      }
    }

    // find unvisited vertex
    for (int j = 1; j <= n; ++j)
    {
      if (visited[j] == false)
      {
        unvisited_vertex = j;
        break;
      }
    }

    delete [ ](visited+1);
    return unvisited_vertex;
  }
}
// File: opttour.cpp
#include <iostream>
#include <cstdlib>
#include <vector>
#include "travel2.h"  // Provides trave2( ) method
#include "pqueue.h" // Provides priorty queue
#include "graph.h"  // Provides graph
using namespace std;
using namespace algorithms;

int main( )
{
  // Graph initialization
  graph example;
  example.set_vertex("V1");
  example.set_vertex("V2");
  example.set_vertex("V3");
  example.set_vertex("V4");
  example.set_vertex("V5");
  // from V1 to Vn
  example.set_edge(1, 2, 14);
  example.set_edge(1, 3, 4);
  example.set_edge(1, 4, 10);
  example.set_edge(1, 5, 20);
  // from V2 to Vn
  example.set_edge(2, 1, 14);
  example.set_edge(2, 3, 7);
  example.set_edge(2, 4, 8);
  example.set_edge(2, 5, 7);
  // from V3 to Vn
  example.set_edge(3, 1, 4);
  example.set_edge(3, 2, 5);
  example.set_edge(3, 4, 7);
  example.set_edge(3, 5, 16);
  // from V4 to Vn
  example.set_edge(4, 1, 11);
  example.set_edge(4, 2, 7);
  example.set_edge(4, 3, 9);
  example.set_edge(4, 5, 2);
  // from V5 to Vn
  example.set_edge(5, 1, 18);
  example.set_edge(5, 2, 7);
  example.set_edge(5, 3, 17);
  example.set_edge(5, 4, 4);

  travel2(example.get_size( ), example, tsp, min);
  cout << "minlength: " << min << endl;
  cout << "[";
  for (itr = tsp.begin( ); itr != tsp.end( ); ++itr)
    cout << *itr <<", ";
  cout << "]" << endl;

  return EXIT_SUCCESS;
}


Time Complexity Analysis

Worst-Case Time Complexity

  • $O(n) = 1 + (n-1) + (n-1)(n-2) + … + (n-1)(n-2)…(n-k) = n!$

현 여행경로에서 미방문정점들을 하나씩 추가하며 상태공간트리를 구축한다. 따라서 상태공간트리 내 전체 노드의 수는 최대 $n!$개가 된다. 최악의 경우 방문하는 노드의 총 수는 계승으로 지수보다 나쁘다. 하지만 가지치기를 통해 상태노드의 수를 줄일 수 있기 때문에 알고리즘의 효율은 더 좋을 수 있다.

Share